Summary
This paper provides a brief overview of the field of agoric software, discusses an example in detail, and suggests avenues for future exploration and experimentation.
Acknowledgements
AgoricNim was developed by the XpNewYorkCity user group as part of a running experiment practicing Extreme Programming on Monday nights. Contributors were Bill Anderson, Michael Harrison, Frank Hilf, Elizabeth Wiethoff, and Adam Wildavsky.
What is
Agoric software?
Agoric software is software that is organized internally using markets to establish prices, where software agents compete for access to resources and for the right to solve problems or sub-problems. In contrast traditional software is organized exclusively using command and control principles, where the actions of the program are under some centralized control. Centralized control may be a feature of some agoric systems, including the example put forward here, but it is not the dominant one.
Agoric software is distinct from Genetic Algorithms, though the two can be combined. Agoric software is modeled on economic processes, rather than biological evolution, and does not include the concept of random mutation.
Why Agoric software?
Human societies can be organized using the principle of command and control, e.g. Communist or totalitarian regimes in general, or using principles permitting individuals and associations of individuals freedom of action, such as Laissez-faire Capitalism. In human societies it is the latter that have proven more successful and productive. It seems worth speculating, then, whether free market principles might also be applied to the field of software.
The case for agoric software, though, is not nearly so strong as the case for freedom in human endeavors, because there can be no moral argument that a software agent ought to have freedom of action. Any argument for agoric software must proceed from practical grounds, by showing that such software is possible, that it can produce useful results, and that the software is reasonably efficient in producing any results that could also be obtained through traditional software.
History of Agoric Software
The field of Agoric software was explicitly identified and named by Mark S. Miller and K. Eric Drexler in a series of papers published in 1988. [Miller88]
Some Agoric concepts were identified earlier, for instance by MIT Professor Tom Malone. [Mallone87, Mallone88]
The height of media attention on Agoric systems seems to have been an article in Wired Magazine [Sidell96].
Why AgoricNim?
In April 2004 the XpNewYorkCity [XpNyc] group was looking for a new open source project to work on in order to practice our Extreme Programming skills. We also wanted to learn about agoric software and settled on one of the simplest problems we could think of, the game of Nim. A game is a useful problem to model because the goal is explicit. Applying the XP principle of “Do the simplest thing that could possibly work” [DTSTTCPW] in an unconventional context we decided to model this simple game and to hope that our approach could subsequently be extended to more complex games and to problem domains that were not games at all.
Rules of Nim
Nim is a game for two players. The players alternate turns, the first player being chosen arbitrarily. The game board consists solely of a number of identical tokens, called stones in honor of early physical implementations of the game. Our initial implementation uses 10 stones. At his turn each player chooses a number of stones to remove from the board. In our initial implementation he may choose one or two stones. The player who takes the last stone loses.
In order to use an internal market the game must have financial consequences. We choose to have the loser of the game pay the winner one unit of currency. This currency is internal to the system, and may, but need not, correspond to a real world currency.
Optimal strategy for Nim
The optimal strategy for this game is straightforward. A winning move will leave one’s opponent on play where the number of stones in the pile is one plus an integral multiple of three. Since we know this strategy in advance in a sense that makes the system we have built precisely useless. We chose to develop the software as if we did not know this optimal strategy, in the hope that the system would in effect learn to play optimally and also produce artifacts sufficient to allow us to deduce the winning strategy. In the future we hope that agoric systems will help us to solve problems that we did not know how to solve in the first place.
It is helpful to have a perfect strategy coded for use in writing tests:
def perfectMove(position)
case position % 3
when 0 then 2
when 1 then nil
when 2 then 1
end
end
Listing 1. “Perfect”
playing strategy
The test code is in a separate file from the program code and is not referenced by the program code, so there is no possibility that a Player can accidentally “cheat” by calling this function.
Other game playing algorithms
An ideal strategy for our simple version of Nim, with only ten pieces, could be produced by any of a number of well-known approaches. Two of these are minimax tree analysis and backtracking [Winston92]. These approaches, however, do not scale well. They would be impractical, for instance, in playing Nim with 1,000,000 pieces. Our initial agoric approach is no better in that regard, but we believe that it is potentially useful all the same. An agoric system can, for instance, be used to choose between several strategies or variations of strategies suggested by humans.
Development approach
Methodology
The AgoricNim team used the Extreme Programming methodology [XP]. That is surely not necessary for developing agoric software, but it worked well for us.
Language
The source code is written in Ruby, a multi-platform object-oriented scripting language. <https://ruby-lang.org>
Open Source
AgoricNim is an open source project using the MIT open source License [MIT]. AgoricNim is hosted by RubyForge [RubyForge].
Measure of effort
The AgoricNim team has spent about 24 hours on the project to date over a period of several months. We work in pairs or occasionally triples, so this represents about 56 person-hours.
Problem decomposition
While our goal is to have the system play a game, it was important to realize that Nim, in common with many games, in fact consists of a series of moves, and that the problem of playing the game well can be reduced to the problem of making the best move in any given position.
Theory of operation in brief
Positions in games will be auctioned off, starting with the initial position. Objects that we call Players will bid for the right to make a move in a game. Upon winning an auction a Player will take a seat in a game, paying the Player who was there previously the amount of the winning bid. He will then make a move. The process continues in this fashion until the game is finished, upon which the losing Player will pay the winning Player one unit of currency. Then a new game is started and the process continues.
Over time good strategies ought to drive out bad, as poor strategies will result in financial loss. A player with no currency is not allowed to place a bid, so over time players employing these poor strategies will cease to have an influence on the course of the game.
Buying and selling positions in games often happens in human games that are played for money, for instance in Backgammon. It is also one way of viewing a financial market such as the stock market.
Measuring Learning
We use two sets of criteria for assessing how much the system has learned.
Our weak learning criteria require that the system will always supply a bidder for a winning position, that that bidder will make the optimal move, and that no player will bid on a losing position.
Our strong learning criteria require the weak criteria, and in addition that every Player who would make an inferior move have zero or negative funds. The weak criteria do not entail the strong criteria because a player with a poorly matched bidding and playing strategy might never win an auction. This could be because he was outbid, or due to the nature of the tie breaking strategy in effect.
Sealed Bid Auctions
In order to simplify the implementation we use sealed bid auctions [Reynolds96] rather than the “open outcry” type that the word auction normally brings to mind. At each turn of the game every Player is given a single opportunity to bid on the position. The position is awarded to the highest bidder, who pays the amount of his bid. We experimented with three different approaches for choosing a winning bidder in case of a tie. The approaches have varying degrees of effectiveness.
A scenario with more detail
The GameShell, the object that controls proceedings, starts by generating two Shills, or house players. These Shills exist to simplify the implementation and to ensure “conservation of currency.” Neither of these Shills will ever bid or make a move -- their only purpose is to sell their position in the game and retire from the fray.
There are 10 simple bidding strategies, one for each possible position in a game, and 2 moving strategies, one which makes each legal move. These strategies are not in the least intelligent – they are almost caricatures of strategies. The GameShell generates a pool of 20 players representing the Cartesian product – each Player has a distinct combination of one bidding and one playing strategy.
The GameShell registers each player with the Auctioneer and then generates a series of NimGames pitting the two Shills against one another – we’ll call their positions East and West, with East to move first. The Auctioneer then conducts an auction for the initial position in the game, awarding it to the highest bidder. Ties are resolved by one of several tie-breaking strategies. The winning bidder pays the existing East player, takes the East seat himself, and makes a move. Next the West position is auctioned in the same manner. When the East position is auctioned again the proceeds go to the Player who purchased the East position on the previous round of the auction. This continues until the game is over, whereupon the loser pays off the winner.
Since the winner of the game can gain at most one unit of currency it would not make sense to bid more than one unit for any position, and we do not instantiate any bidding strategies that do so.
Each player object will do well in financial terms if, over time, it is able to sell its positions for as much as or more than it paid for them, or if it purchases a position which leads to an immediate win. If on the other hand it pays more for positions than it is able to sell them for or simply loses the games containing the positions it purchases then it will deplete its funds over time, eventually going broke. Players with no currency are not permitted to place bids.
Initially the results will seem random, since the strategies were not chosen for their intelligence. When we repeat the process over time, however, we see the effects of the marketplace. Players with poor strategies will tend to go broke – eventually only sound strategies will remain. By examining the states of the players after several iterations we can learn which combinations of bidding and playing strategies proved successful. Further, even without examining the players, we can use the system to play a game against an external entity, either human or another piece of software. In effect it will have learned how to play well.
This learning is analogous to the learning that takes place in a free economy, where (in the absence of government bailouts) firms that are inefficient or continue to manufacture obsolete projects tend to go out of business whereas their more nimble competitors survive and so continue to influence the economy.
Termination criteria
When we introduce variations into the process, such as different kinds of auctions, it will often be with the goal of discovering the effect of the game on the pace of learning. In order to do so we will need to be able to measure the pace of learning. Our initial experiments suggested that one effective way to do this is to wait for one of the Shills to be forced to make a move. Since the Shills never bid a Shill will have to make a move only if no one else bids on its position. If no one bids on a position the position must be a losing one – every player who was willing to bid on the position has gone broke. Accordingly if a Shill is forced to make a move he simply resigns. The GameShell notes the resignation and terminates its game creation loop, then reports its results.
Breaking Ties
Whether and how much the system learns turns out to be dependent on the mechanism the Auctioneer uses to choose the winning bidder for a position in case of a tie. In the system’s initial state each position attracts bids of equal amounts from two Players, so ties are common.
An Auctioneer can use three different tie-breaking strategies. These strategies are implemented using the Strategy pattern [GOF95] so they are represented by three Classes. An instance of one of these classes is passed to the Auctioneer’s constructor.
The simplest and default strategy is to award the tie to the first bidder in the Auctioneer’s list of Players. This is arbitrary but does produce a system that learns. Another strategy is to award ties by lot. This turns out to have serious deficiencies. A third strategy is to award ties to the bidder who won an auction least recently. This strategy allows the system to demonstrate the most dramatic pattern of learning.
Show Me The Learning
Figure 1 shows the initial resources of the Players instantiated by the GameShell. Each column represents a Player. In each pair of columns the Player whose MoveStrategy requires it to take one stone is on the left. The Auctioneer will use the BreakTiesByTimeStrategy, the one we’ve found most effective.
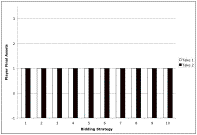
Figure 1. Initial Currency Allocations
Figure 2 shows that after five games some Players are already out of business.
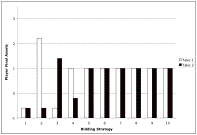
Figure 2.
Currency Allocations after Five Games using BreakTiesByTimeStrategy
After 10 games things have shaken out further.
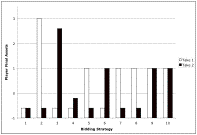
Figure 3. Currency Allocations after Ten Games using BreakTiesByTimeStrategy
The system terminates after 15 games. The resulting currency allocations are shown in Figure 4.
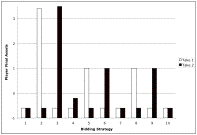
Figure 4. Final Currency Allocations using BreakTiesByTimeStrategy
As we would hope, there are no solvent Players left willing to bid on positions 1, 4, 7, and 10, each of which is a losing proposition. In each of the other positions one Player has either prospered or at any rate retained its initial allocation of funds, while the other player is bankrupt. This demonstrates that the system satisfied our strong learning criteria when using the BreakTiesByTimeStrategy.
Effectiveness of learning
Rather than examining Player resources we can look at the system as a black box and simply ask, given a tiebreak strategy and a number of games, what moves the resulting system would make. Here is the program output showing the moves that would be made at the stages corresponding to the four diagrams above. An “x” indicates that no Players are willing to bid on the position in question.
% ./nim.rb -breakTiesByTime 0
Position: 1 2 3 4 5 6 7 8 9 10
Move: 1 1 1 1 1 1 1 1 1 1
% ./nim.rb -breakTiesByTime 5
Position: 1 2 3 4 5 6 7 8 9 10
Move: x 1 2 1 2 1 2 1 2 2
% ./nim.rb -breakTiesByTime 10
Position: 1 2 3 4 5 6 7 8 9 10
Move: x 1 2 x 1 2 1 1 2 1
% ./nim.rb -breakTiesByTime 20
Terminated after 15 games.
Position: 1 2 3 4 5 6 7 8 9 10
Move: x 1 2 x 1 2 x 1 2 x
Results using other tie break criteria
Using stochastic tie-break criteria can produce inferior results. Here are the results of two runs using a strategy that breaks ties by awarding the position at random to one of the high bidders. The command line switch –srand lets us change the value Ruby uses as the seed for its pseudo-random number generator for each run.
% ./nim.rb -breakTiesByLot -srand 1
Terminated after 15 games.
Position: 1 2 3 4 5 6 7 8 9 10
Move:
x 1 2 x 1 2 x 1 2 x
% ./nim.rb -breakTiesByLot -srand 5
Terminated after 13 games.
Position: 1 2 3 4 5 6 7 8 9 10
Move: x 1 2 x 1 1 x 2 2 x
The second set of output is sufficient to show that BreakTiesByLotStrategy does not satisfy even our weak learning criteria.
An arbitrary but predictable tiebreak strategy appears more promising. Here’s its output. It is the system’s default strategy, so it is not specified on the command-line.
% ./nim.rb
Terminated after 12 games.
Position: 1 2 3 4 5 6 7 8 9 10
Move: x 1 2 x 1 2 x 1 2 x
This strategy converges faster than our other strategies. Figure 5, though, shows that it does not satisfy our strong learning criteria. Players with unsuccessful strategies are still solvent where the number of pieces is 2, 5, or 8, all of which are winning positions.
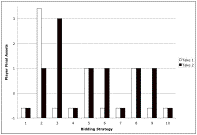
Figure 5. Final Currency Allocations using FirstInListTieBreakStrategy
Dimensions for Expansion
The functionality of the software can be expanded along a number of dimensions, some trivial, some ambitious.
Human Participation
We ought to let a person play against the system, either before, during, or after it has trained by playing against itself. The implementation of this in game terms is straightforward – we need only choose a user interface.
Simple Nim Variations
There are a number of features we could add without changing the nature of the game. For instance the initial number of stones can be modified, or the minimum and maximum stones per more. We can change the winning criterion so that the player who takes the last stone wins.
Auction Variations
Experimenting with different implementations of the auction can not only satisfy our curiosity, but also can let us experiment and determine whether one or another auction format might speed the system’s learning.
One promising change is to experiment with different types of auctions, and in particular a Vickrey Auction [Vickrey], where the winning bidder pays the price named by the second highest bidder.
We also plan to experiment with different methods of breaking ties. One possibilities is to award the game to all the winning bidders at once, either by cloning the game at its full stake or by cloning the game and dividing the stake by the number of winning bidders.
Another experiment would involve introducing financial friction. The auctioneer could require a commission, as is usually the case in real life auctions.
User Interface
Adding a GUI and/or a web front end would allow more people to play with the system. Suggestions from users might then lead to further enhancement s suggestions for experiment. The interface could also be treated as a meta-game, where the object is to make learning happen as fast as possible by adjusting various parameters.
Once we add a UI we might also find a demand for persistence, since users might want to save the state of a system once they have “trained” it, or rather allowed it to train itself.
GameShell Variations
Currently the game shell is seeded with players who, when they bid, bid .6 units of currency. We can both reduce and increase the number of bidding quanta, making for more interesting auctions. Initially we used two quanta, .3 and .6. This turned out to be unnecessary and had three deleterious effects. One was that we needed to play more games before the system learned all it could. Another was that with twice as many players results were harder to interpret. A third was that some low bidders with unsuccessful strategies would remain solvent. They would in effect be shielded by higher bidders with successful strategies.
Another possibility is to introduce a perfect player into the game – one would suppose that that would increase the pace of learning.
One experiment begging to be performed is to examine the system’s performance when the initial position is a winning one rather than a losing one.
One interesting change to the GameShell would be to seed the Auctioneer with additional players representing more sophisticated but still non-optimal strategies. For instance we could add a Player with an optimal strategy for larger positions, but a poor strategy for small positions. This Player would help us win a game with an arbitrarily large initial number of stones, but it could not succeed without the aid of the players who bid on small fixed positions. This change could show that the system can be used to combine strategies for games that require different approaches to different kinds of positions. When writing a chess program, for instance, we might use an agoric system to help decide when an end-game algorithm should take over from a middle-game algorithm.
Other Games
There are more interesting Nim variations we could model, in particular one where there is more than one pile of stones. This variation in fact requires a different end-game strategy than it does for the rest of the game. We could also model games which are still simple, say Tic-Tac-Toe, but which allow ties.
Nothing in our approach need restrict us to two-player games. The same approach of auctioning off positions in a game will work equally well (or equally poorly) for single-player or multi-player games.
Other Development Architectures
One reason we started working on AgoricNim was with the idea of eventually running the auctions in multiple processes simultaneously, and then on multiple processors and multiple machines. This would likely be counter-productive with the simple bidding and playing strategies we have currently, but could be a powerful technique to arbitrate between complex strategies for more complex games such as Chess. A competent Chess program, for instance, might be produced by using auctions to choose between moves proposed by different programs running on different machines.
Conclusions
The initial implementation does not make as much use of its market as we’d hoped initially. It was a particular disappointment that having Players with differing bid amounts did not enhance the system’s effectiveness. The market is in effect acting as an array where losing decisions are tracked so as not to be repeated. To see a more dynamic market we’ll need to model a slightly more sophisticated game.
All the same, Agoric software has the potential to produce results of interest both academically and commercially. We’ve shown that Agoric experiments can be performed with minimal machine and developer resources – the field is ripe for future exploration and exploitation.